Abstract
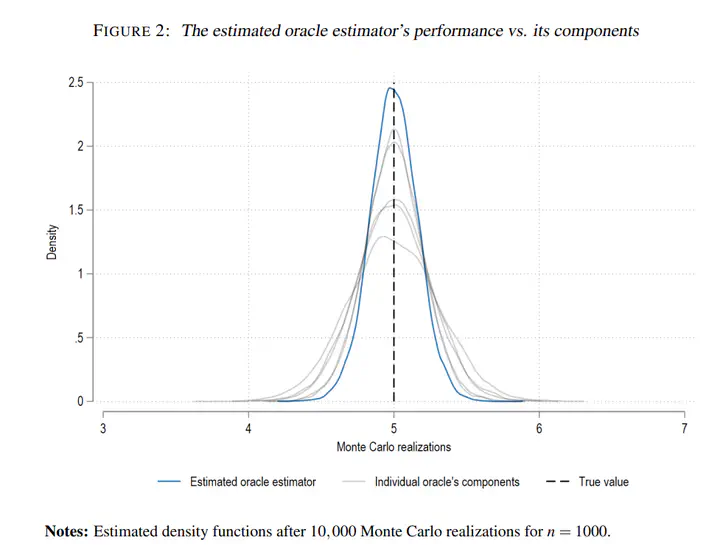
This paper introduces a new estimator for continuity-based Regression Discontinuity (RD) designs named the estimated Oracle Local Polynomial Estimator (OLPE). The OLPE is a weighted average of a collection of local polynomial estimators, each of which is characterized by a unique bandwidth sequence, polynomial order, and kernel weighting schemes, and whose weights are chosen to minimize the Mean-Squared Error (MSE) of the combination. This procedure yields a new consistent estimator of the target causal effect exhibiting lower bias and/or variance than its components. The precision gains stem from two factors. First, the method allocates more weight to estimators with lower asymptotic mean squared error, allowing it to select the specifications that are best suited to the specific estimation problem. Second, even if the individual estimators are not optimal, averaging mechanically leads to bias reduction and variance shrinkage. Although the OLPE weights are unknown, an “estimated” OLPE can be constructed by replacing unobserved MSE-optimal weights with those derived from a consistent estimator. Monte Carlo simulations indicate that the estimated OLPE can significantly enhance precision compared to conventional local polynomial methods, even in small sample sizes. The estimated OLPE remains consistent and asymptotically normal without imposing additional assumptions beyond those required for local polynomial estimators. Moreover, this approach applies to sharp, fuzzy, and kink RD designs, with or without covariates.